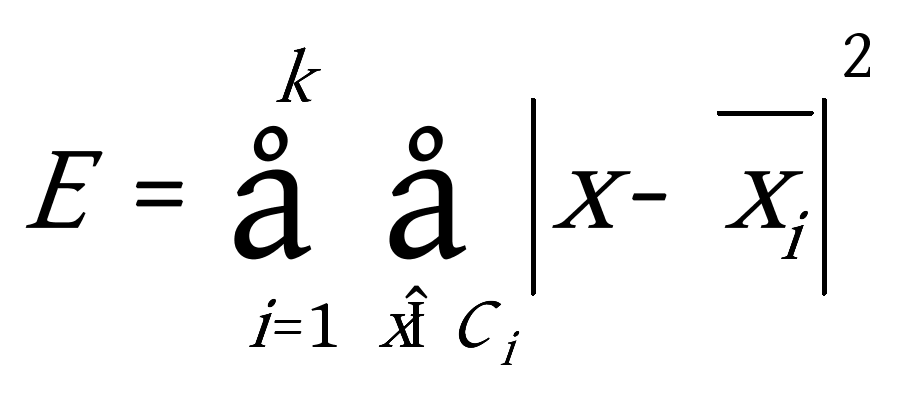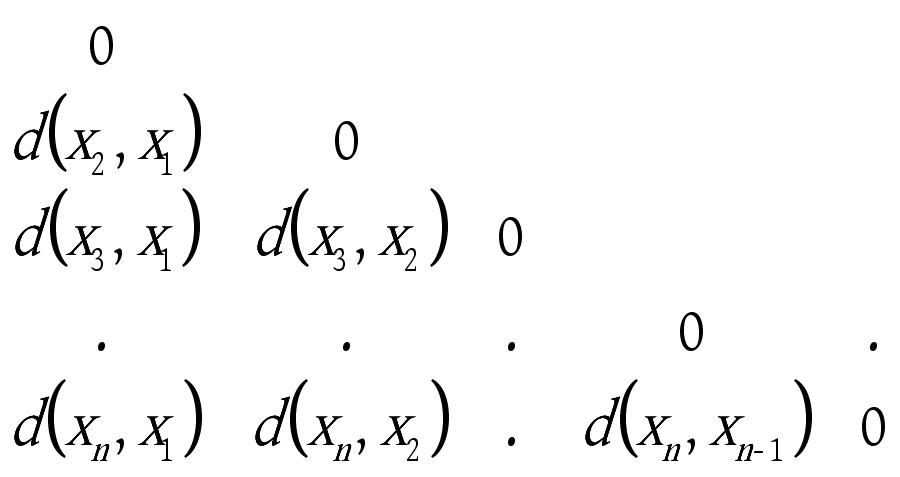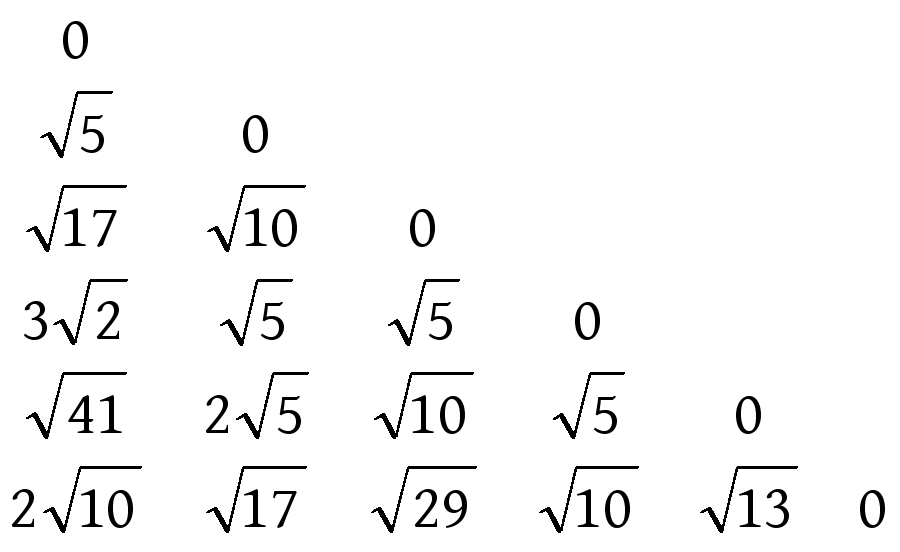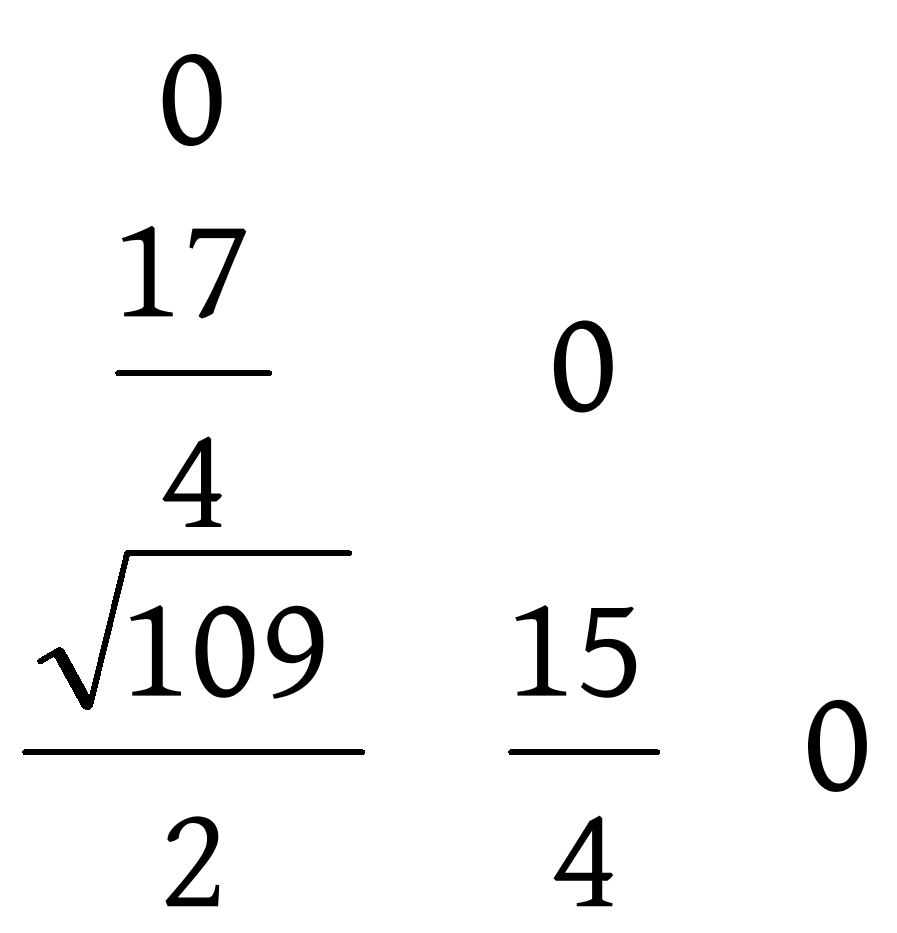知识库 : 聚类分析

与大家分享一些数据挖掘方面的内容，目前我们DM Studio中有许多聚类算法，选取了 Kmeans方法，首先全面剖析Kmeans方法的优缺点，然后推荐几种的改进后的聚类算法。DM studio产品成型后，关于以后如何改进聚类算法，为用户创造更大价值方面有比较深的启示。大家若有想法或意见，欢迎一起交流学习。

1.数据挖掘与聚类分析

数据挖掘是一种提取出隐含在大量数据中的潜在的、有用的信息并被人们识别、处理的数据库中的知识发现(Knowledge Discovery in Database)。数据挖掘技术结合了模式识别、数据库、统计学、机器学习和人工智能等多个领域的一种新兴的交叉的学科技术。数据挖掘有多个研究方向，分类、聚类、关联规则挖掘等。聚类分析是数据挖掘领域中的一个比较热门的研究方向。聚类分析是要达到这样一种目的，将数据对象进行划分成不同的簇使得同一个簇中的数据对象具有较高的相似度，不同簇中的数据对象的相似度较低。
目前为止,聚类分析算法一般有以下五种分类:基于划分的聚类算法、基于层次的聚类算法、基于密度的聚类算法、基于网格的聚类算法和基于模型的聚类方法。

2.Kmeans方法简介

K均值聚类算法是由 J.B.MacQueen 在 1967 年提出的。K均值聚类算法是一种经典的划分聚类算法，是到目前为止应用最广泛最成熟的一种聚类分析方法。它属于基于距离的聚类算法，所谓的基于距离的聚类算法指采用距离作为相似性度量的评价指标，也就是说，当两个对象离的近，二者之间的距离比较小，那么它们之间的相似性就比较大。K均值聚类算法具有简单快速、适于处理大数据集等优点，目前，已被广泛应用于科学研究和工业应用中。
K均值聚类算法的基本思想：K均值聚类算法属于一种动态聚类算法,也称作逐步聚类法,算法首先随机选取k个点作为初始聚类中心，然后计算各个数据对象到各聚类中心的距离，把数据对象归到离它最近的那个聚类中心所在的类，对调整后的新类计算新的聚类中心，如果相邻两次的聚类中心没有任何变化，说明数据对象调整结束，聚类准则已经收敛。本算法的一个特点是在每次迭代中都要考察每个样本的分类是否正确，若不正确，就要调整。在全部数据调整完后，再修改聚类中心，进入下一次迭代。如果在一次迭代算法中，所有的数据对象被正确分类，则不会有调整，聚类中心也不会有任何变化，这标志着已经收敛，至此算法结束。
K均值聚类算法的流程：
输入：簇的数目k和包含n个对象的数据库。
输出：k个簇，使平方误差准则最小。
① Assign initial value for kmeans;//任意选择k个对象作为初始的簇中心；
② Repeat;
③ For j=1 to n DO assign each to the cluster which has the closest distance;//根据簇中对象的平均值，将每个对象赋给最类似的簇
④ FOR i=1 to k DO ;//更新簇的平均值，即计算每个对象簇中对象的平均值
⑤ Compute ;//计算准则函数（有很多聚类准则函数，选取比较常用的平方误差准则）
⑥ UNTIL 不再明显的变化;
K均值聚类算法的优缺点：
K均值聚类算法是一种基于划分的聚类算法，尝试找出使得聚类准则函数值最小的k个划分，当簇与簇之间的特征区别比较明显的时候，并且结果簇是密集的，K均值聚类算法聚类结果的效果较好。K均值聚类算法的优点主要集中在：算法快速、简单；对大数据集有较高的效率并且是可伸缩性的；时间复杂度近于线性，而且适合挖掘大规模数据集。K均值聚类算法的时间复杂度是，其中代表数据集中对象的数量，代表着聚类的数目，代表算法迭代的次数，但是到目前为止，K均值聚类算法也存在着许多缺点，在应用中面临着许多问题，有待于解决，K均值聚类算法存在的主要问题有以下几个方面：
(1)K均值聚类算法中需要用户事先指定聚类的个数k值。
很多时候，在对数据集进行聚类的时候，用户起初并不清楚该数据集应该分多少簇才合适，即聚类个数k值难以估计。有些算法如ISODATA算法是通过簇的自动分裂和合并来得到较为理想的k的簇的个数。如何寻找K值，确定合适的聚类数目有利于提高聚类的精度。
(2)算法对初始值的选取依赖性极大以及算法常陷入局部极小解，随机选择初始中心点，容易导致聚类结果不稳定。
K均值聚类算法首先随机地选取k个点作为初始聚类中心，再利用迭代的重定位技术寻找最优聚类中心直到算法收敛。因此，初始值的不同可能导致算法聚类效果的不稳定。并且，K均值聚类算法常采用误差平方和准则函数作为聚类准则函数（目标函数）。目标函数在空间状态是一个非凸函数，非凸函数往往存在很多个局部极小值，只有一个是全局最小。由于算法每次开始选取的初始聚类中心落入非凸函数曲面的位置，有很大可能会偏离全局最优解的搜索范围，因此通过迭代运算，目标函数常常达到局部最小而难以得到全局最小，如下图显示的非凸函数。目标函数的搜索方向总是沿着误差平方和准则函数减小的方向进行。不同的初始中心使得聚类中心向量沿着不同的路径使目标函数减小，目标函数分别沿、、、四种不同的初始聚类中心的路径逐步减小，分别找到各自的最小值。其中，只有从开始迭代的最小值才是全局最小点，而、、对应的最小值则是局部极小点。K均值聚类算法是一种爬山算法(Hill climbing)，算法停止时常常找到的是局部极小值。
A B C D
(3)K均值聚类算法对噪声数据和孤立点数据较为敏感。
从K均值聚类算法的聚类过程我们知道，簇的中心的每一次更新都是通过计算簇内所有数据对象的均值获得的，而噪声数据和孤立点数据通常是远离数据样本空间的密集区域，如果将噪声数据和孤立点数据加入到簇的中心的更新计算中，则势必对簇的中心的计算产生重要影响，甚至有可能使新计算出来的簇中心严重偏离数据样本空间的密集区域，以这样的簇中心进行聚类将对聚类结果产生极为不利的影响。
(4) K均值聚类算法一般只能发现球状簇。
K均值聚类算法是一种硬聚类算法，通常采用采用欧氏距离作为数据样本间相似性的度量方法，算法的目标函数通常采用误差平方和函数，这种目标函数对于处理数据样本分布比较集中且各类中的数据样本的数量相差不大的数据集效果较好。但是当处理各类中数据样本数量悬殊较大、各类边界区分模糊且各类的形状差异较大的数据集时，为了使目标函数的最小化，有可能会将一个较大的类分割成若干个小的类。这会使聚类结果变得不理想。
(5)对于大数据量，算法的开销非常大。
从K均值聚类算法流程可以看出，该算法需要不断地进行样本分类迭代调整，不断地计算调整后的新的聚类中心。因此，当数据集的数量非常大时，算法的时间开销也是相当惊人的的。所以需要对算法的时间复杂度进行分析、改进，以提高算法的应用范围。

3.基于网格的赫夫曼树算法

曾经有学者提出了一种基于赫夫曼树的聚类算法，算法首先会根据相异度矩阵构造赫夫曼树，然后根据赫夫曼树选择聚类算法的初始中心，避免随机选取初始中心点而导致聚类结果的不稳定性，同时在一定程度上减少了算法陷入局部最优解的可能，但是当数据集比较大时，该算法计算时间着实不小，而且易受噪声数据的干扰，在现实生活中，有些孤立点是无需考虑的，比如超市为了扩大规模，在聚类中心点建立分店，将分店的效益，构建分店所需要的经费综合考虑，我们就无需将一些偏僻的地点考虑。
针对上述缺点，在此提出了一种基于网格的赫夫曼树聚类算法，该算法将基于网格的聚类算法与基于赫夫曼树聚类算法相结合。基于网格方法的聚类算法对数据集大小具有好的可伸缩性，能处理大规模数据集。由于聚类算法的所有操作都在网格单元上进行，在将数据读入网格数据结构之后，算法的处理时间就与数据点数目无关，而只与网格单元个数有关。在基于网格方法的聚类算法中，算法使用相连的网格单元表示簇，因此算法对簇的形状与簇的大小没有任何限制。算法其它的优点包括聚类结果不受数据输入顺序影响，且结果的表达直观、易于理解。基于赫夫曼树聚类算法简单方便，提高初始聚类中心选取的稳定性，进而可以提高聚类结果的有效性。基于网格的赫夫曼树聚类算法首先会将数据点分配到各网格，计算各个网格中的密度，我们仅对网格密度大于给定阈值的网格进行操作，其余的网格中的数据点当做"噪声"处理，然后选取各个网格的中心构建赫夫曼树，这样大大减少了计算量并且可以得到比较好的聚类结果。
那么如何构造赫夫曼树呢？赫夫曼最早给出了一个带有一般规律的算法，俗称赫夫曼算法。叙述如下：
(1)根据给定n个权值构成n棵二叉树的集合，其中每棵二叉树中只有一个带权的根节点，其左右子树均空。
(2)在中选取两棵根节点的权值最小的树作为左右子树构造一棵新的二叉树，且置新的二叉树的根节点的权值为其左右子树上根节点的权值之和。
(3)在中删除这两棵树，同时将新得到的二叉树加入中。
(4)重复(2)和(3)，直到只含一棵树为止，这棵树便就是赫夫曼树。
算法的时间复杂度主要取决于步骤(2)，步骤(2)主要来寻找每次最小的两个权值，它一般进行次比较。之后每当产生时，只需在新序列中进行插入运算，其复杂度是，由于总共进行了次迭代，因此整个算法的时间复杂度是。
相异度矩阵：由n个数据对象构成的数据集为，用表示数据象和之间的差异程度，可以用如下表示所有数据对象两两间差异程度的n×n矩阵来表示该数据集，这样的矩阵称为相异度矩阵，如下：

通常为一非负数，一般采用欧氏距离，其值的大小直接反映数据对象和之间的相异程度。其值越大，反映两数据对象间的相异程度越大，相反，其值越小，则反映两数据之间的相异程度越小，显然： = ， =0。因此，相异度矩阵是一个斜三角矩阵。
下面给出利用相似度来构建赫夫曼树的一个简单的实例，假设有这么一组数据：，需要将这6个点分为三类，过程如下：
1)首先根据欧氏距离建立相似度矩阵，矩阵如下：

2)找到矩阵中的最小值，也就是数据点与的相似度，计算这两个点的均值，即，在数据集中删除与，将平均值加入到数据集中，即此时的数据集为：，计算此时数据集的相似度矩阵，矩阵如下：

3)找到此时矩阵中的最小值，即数据与的相似度，计算这两个点的均值，即，在数据集中删除与，将平均值加入到数据集中，即此时的数据集为：，计算此时的相似度矩阵，矩阵如下：

3)重复上述迭代过程，直到数据集中只剩下一个数据点，相似度矩阵的迭代过程如下图，赫夫曼树的构造过程如下图：

算法思想
基于网格的赫夫曼树聚类算法大体上分为四步：
1.基于网格的赫夫曼树聚类算法主要针对比较大的数据集，在构建赫夫曼树之前首先以数据中心点为中心,对整个数据空间进行划分，将所有的数据分配到对应的区域中,并计算出新区域的中心点,对新的区域重新进行划分,形成更多的网格，划分网格的多少与给定的数据集大小有关，如图4.3，根据设定的密度阈值，计算出各个密集网格，每个网格的中心点作为代表点，将其作为形成聚类的基础。
1)当时，进行一次划分，形成4个区域。
2)当时，进行二次划分，形成16个区域。
3)当时，我们一般对其进行第三次划分，形成64（或32）个区域。

2.根据赫夫曼树的思想与相异度矩阵，将数据样本构造成一棵树，构造赫夫曼树的过程如图4.2。
3.对于构造出来的赫夫曼树，按构造结点的逆序找到个结点，去掉这，我们可以得到棵子树，棵子树的个均值即初始的个聚类中心点，如上例，删除与两个结点，我们即可以得到三棵子树，计算着三棵子树的均值即为初始聚类中心点。
4.对于已经得到的个初始聚类中心点，我们用均值聚类算法进行聚类，将数据空间划分为个聚类。
直到今天有许许多多的关于聚类分析的算法，以及相应的改进算法，基于网格的（密度的）最小生成树算法、基于网格的（密度的）赫夫曼树算法是我认为比较好的两种改进聚类算法，该两种算法将基于网格、密度、划分的聚类分析算法相融合，有效的解决了划分算法只能发现球状簇、易受噪声数据影响的缺点。限于篇幅，没有贴出算法的时间复杂度、具体对比过程。总的来说改进后的聚类算法能极大地提升聚类分析的效率与准确率。

知识库 : 聚类分析

1.数据挖掘与聚类分析

2.Kmeans方法简介

3.基于网格的赫夫曼树算法

Attachments: