第三章:列表¶
列表是 Lisp 的基本資料結構之一。在最早的 Lisp 方言裡,列表是唯一的資料結構: “Lisp” 這個名字起初是 “LISt Processor” 的縮寫。但 Lisp 已經超越這個縮寫很久了。 Common Lisp 是一個有著各式各樣資料結構的通用性程式語言。
Lisp 程式開發通常呼應著開發 Lisp 語言自身。在最初版本的 Lisp 程式,你可能使用很多列表。然而之後的版本,你可能換到快速、特定的資料結構。本章描述了你可以用列表所做的很多事情,以及使用它們來示範一些普遍的 Lisp 概念。
3.1 構造 (Conses)¶
在 2.4 節我們介紹了 cons , car , 以及 cdr ,基本的 List 操作函數。 cons 真正所做的事情是,把兩個物件結合成一個有兩部分的物件,稱之爲 Cons 物件。概念上來說,一個 Cons 是一對指標;第一個是 car ,第二個是 cdr 。
Cons 物件提供了一個方便的表示法,來表示任何型別的物件。一個 Cons 物件裡的一對指標,可以指向任何型別的物件,包括 Cons 物件本身。它利用到我們之後可以用 cons 來構造列表的可能性。
我們往往不會把列表想成是成對的,但它們可以這樣被定義。任何非空的列表,都可以被視爲一對由列表第一個元素及列表其餘元素所組成的列表。 Lisp 列表體現了這個概念。我們使用 Cons 的一半來指向列表的第一個元素,然後用另一半指向列表其餘的元素(可能是別的 Cons 或 nil )。 Lisp 的慣例是使用 car 代表列表的第一個元素,而用 cdr 代表列表的其餘的元素。所以現在 car 是列表的第一個元素的同義詞,而 cdr 是列表的其餘的元素的同義詞。列表不是不同的物件,而是像 Cons 這樣的方式連結起來。
當我們想在 nil 上面建立東西時,
> (setf x (cons 'a nil))
(A)
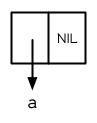
圖 3.1 一個元素的列表
產生的列表由一個 Cons 所組成,見圖 3.1。這種表達 Cons 的方式叫做箱子表示法 (box notation),因爲每一個 Cons 是用一個箱子表示,內含一個 car 和 cdr 的指標。當我們呼叫 car 與 cdr 時,我們得到指標指向的地方:
> (car x)
A
> (cdr x)
NIL
當我們構造一個多元素的列表時,我們得到一串 Cons (a chain of conses):
> (setf y (list 'a 'b 'c))
(A B C)
產生的結構見圖 3.2。現在當我們想得到列表的 cdr 時,它是一個兩個元素的列表。

圖 3.2 三個元素的列表
> (cdr y)
(B C)
在一個有多個元素的列表中, car 指標讓你取得元素,而 cdr 讓你取得列表內其餘的東西。
一個列表可以有任何型別的物件作爲元素,包括另一個列表:
> (setf z (list 'a (list 'b 'c) 'd))
(A (B C) D)
當這種情況發生時,它的結構如圖 3.3 所示;第二個 Cons 的 car 指標也指向一個列表:
> (car (cdr z))
(B C)
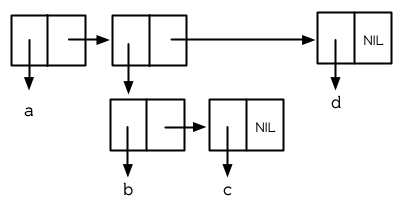
圖 3.3 巢狀列表
前兩個我們構造的列表都有三個元素;只不過 z 列表的第二個元素也剛好是一個列表。像這樣的列表稱爲巢狀列表,而像 y 這樣的列表稱之爲平坦列表 (flatlist)。
如果參數是一個 Cons 物件,函數 consp 返回真。所以我們可以這樣定義 listp :
(defun our-listp (x)
(or (null x) (consp x)))
因爲所有不是 Cons 物件的東西,就是一個原子 (atom),判斷式 atom 可以這樣定義:
(defun our-atom (x) (not (consp x)))
注意, nil 既是一個原子,也是一個列表。
3.2 等式 (Equality)¶
每一次你呼叫 cons 時, Lisp 會配置一塊新的記憶體給兩個指標。所以如果我們用同樣的參數呼叫 cons 兩次,我們得到兩個數值看起來一樣,但實際上是兩個不同的物件:
> (eql (cons 'a nil) (cons 'a nil))
NIL
如果我們也可以詢問兩個列表是否有相同元素,那就很方便了。 Common Lisp 提供了這種目的另一個判斷式: equal 。而另一方面 eql 只有在它的參數是相同物件時才返回真,
> (setf x (cons 'a nil))
(A)
> (eql x x)
T
本質上 equal 若它的參數打印出的值相同時,返回真:
> (equal x (cons 'a nil))
T
這個判斷式對非列表結構的別種物件也有效,但一種僅對列表有效的版本可以這樣定義:
> (defun our-equal (x y)
(or (eql x y)
(and (consp x)
(consp y)
(our-equal (car x) (car y))
(our-equal (cdr x) (cdr y)))))
這個定義意味著,如果某個 x 和 y 相等( eql ),那麼他們也相等( equal )。
勘誤: 這個版本的 our-equal 可以用在符號的列表 (list of symbols),而不是列表 (list)。
3.3 爲什麼 Lisp 沒有指標 (Why Lisp Has No Pointers)¶
一個理解 Lisp 的祕密之一是意識到變數是有值的,就像列表有元素一樣。如同 Cons 物件有指標指向他們的元素,變數有指標指向他們的值。
你可能在別的語言中使用過顯式指標 (explicitly pointer)。在 Lisp,你永遠不用這麼做,因爲語言幫你處理好指標了。我們已經在列表看過這是怎麼實現的。同樣的事情發生在變數身上。舉例來說,假設我們想要把兩個變數設成同樣的列表:
> (setf x '(a b c))
(A B C)
> (setf y x)
(A B C)
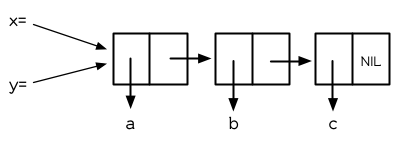
圖 3.4 兩個變數設爲相同的列表
當我們把 x 的值賦給 y 時,究竟發生什麼事呢?記憶體中與 x 有關的位置並沒有包含這個列表,而是一個指標指向它。當我們給 y 賦一個相同的值時, Lisp 複製的是指標,而不是列表。(圖 3.4 顯式賦值 x 給 y 後的結果)無論何時,你將某個變量的值賦給一個變數時,兩個變數的值將會是 eql 的:
> (eql x y)
T
Lisp 沒有指標的原因是因爲每一個值,其實概念上來說都是一個指標。當你賦一個值給變數或將這個值存在資料結構中,其實被儲存的是指向這個值的指標。當你要取得變數的值,或是存在資料結構中的內容時, Lisp 返回指向這個值的指標。但這都在檯面下發生。你可以不加思索地把值放在結構裡,或放“在”變數裡。
爲了效率的原因, Lisp 有時會選擇一個折衷的表示法,而不是指標。舉例來說,因爲一個小整數所需的記憶體空間,少於一個指標所需的空間,一個 Lisp 實現可能會直接處理這個小整數,而不是用指標來處理。但基本要點是,程式設計師預設可以把任何東西放在任何地方。除非你宣告你不願這麼做,不然你能夠在任何的資料結構,存放任何型別的物件,包括結構本身。
3.4 建立列表 (Building Lists)¶
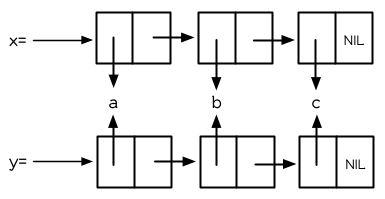
圖 3.5 複製的結果
函數 copy-list 接受一個列表,然後返回此列表的複本。新的列表會有同樣的元素,但是裝在新的 Cons 物件裡:
> (setf x '(a b c)
y (copy-list x))
(A B C)
圖 3.5 展示出結果的結構; 返回值像是有著相同乘客的新公交。我們可以把 copy-list 想成是這麼定義的:
(defun our-copy-list (lst)
(if (atom lst)
lst
(cons (car lst) (our-copy-list (cdr lst)))))
這個定義暗示著 x 與 (copy-list x) 會永遠 equal ,並永遠不 eql ,除非 x 是 NIL 。
最後,函數 append 返回任何數目的列表串接 (concatenation):
> (append '(a b) '(c d) 'e)
(A B C D . E)
通過這麼做,它複製所有的參數,除了最後一個
3.5 範例:壓縮 (Example: Compression)¶
作爲一個例子,這節將示範如何實現簡單形式的列表壓縮。這個算法有一個令人印象深刻的名字,遊程編碼(run-length encoding)。
(defun compress (x)
(if (consp x)
(compr (car x) 1 (cdr x))
x))
(defun compr (elt n lst)
(if (null lst)
(list (n-elts elt n))
(let ((next (car lst)))
(if (eql next elt)
(compr elt (+ n 1) (cdr lst))
(cons (n-elts elt n)
(compr next 1 (cdr lst)))))))
(defun n-elts (elt n)
(if (> n 1)
(list n elt)
elt))
圖 3.6 遊程編碼 (Run-length encoding):壓縮
在餐廳的情境下,這個算法的工作方式如下。一個女服務生走向有四個客人的桌子。“你們要什麼?” 她問。“我要特餐,” 第一個客人說。 “我也是,” 第二個客人說。“聽起來不錯,” 第三個客人說。每個人看著第四個客人。 “我要一個 cilantro soufflé,” 他小聲地說。 (譯註:蛋奶酥上面灑香菜跟醬料)
瞬息之間,女服務生就轉身踩著高跟鞋走回櫃檯去了。 “三個特餐,” 她大聲對廚師說,“還有一個香菜蛋奶酥。”
圖 3.6 示範了如何實現這個壓縮列表演算法。函數 compress 接受一個由原子組成的列表,然後返回一個壓縮的列表:
> (compress '(1 1 1 0 1 0 0 0 0 1))
((3 1) 0 1 (4 0) 1)
當相同的元素連續出現好幾次,這個連續出現的序列 (sequence)被一個列表取代,列表指明出現的次數及出現的元素。
主要的工作是由遞迴函數 compr 所完成。這個函數接受三個參數: elt , 上一個我們看過的元素; n ,連續出現的次數;以及 lst ,我們還沒檢視過的部分列表。如果沒有東西需要檢視了,我們呼叫 n-elts 來取得 n elts 的表示法。如果 lst 的第一個元素還是 elt ,我們增加出現的次數 n 並繼續下去。否則我們得到,到目前爲止的一個壓縮的列表,然後 cons 這個列表在 compr 處理完剩下的列表所返回的東西之上。
要復原一個壓縮的列表,我們呼叫 uncompress (圖 3.7)
> (uncompress '((3 1) 0 1 (4 0) 1))
(1 1 1 0 1 0 0 0 0 1)
(defun uncompress (lst)
(if (null lst)
nil
(let ((elt (car lst))
(rest (uncompress (cdr lst))))
(if (consp elt)
(append (apply #'list-of elt)
rest)
(cons elt rest)))))
(defun list-of (n elt)
(if (zerop n)
nil
(cons elt (list-of (- n 1) elt))))
圖 3.7 遊程編碼 (Run-length encoding):解壓縮
這個函數遞迴地遍歷這個壓縮列表,逐字複製原子並呼叫 list-of ,展開成列表。
> (list-of 3 'ho)
(HO HO HO)
我們其實不需要自己寫 list-of 。內建的 make-list 可以辦到一樣的事情 ── 但它使用了我們還沒介紹到的關鍵字參數 (keyword argument)。
圖 3.6 跟 3.7 這種寫法不是一個有經驗的Lisp 程式設計師用的寫法。它的效率很差,它沒有儘可能的壓縮,而且它只對由原子組成的列表有效。在幾個章節內,我們會學到解決這些問題的技巧。
載入程式
在這節的程式是我們第一個實質的程式。
當我們想要寫超過數行的函數時,
通常我們會把程式寫在一個檔案,
然後使用 load 讓 Lisp 讀取函數的定義。
如果我們把圖 3.6 跟 3.7 的程式,
存在一個檔案叫做,“compress.lisp”然後輸入
(load "compress.lisp")
到頂層,或多或少的,
我們會像在直接輸入頂層一樣得到同樣的效果。
注意:在某些實現中,Lisp 檔案的擴展名會是“.lsp”而不是“.lisp”。
3.6 存取 (Access)¶
Common Lisp 有額外的存取函數,它們是用 car 跟 cdr 所定義的。要找到列表特定位置的元素,我們可以呼叫 nth ,
> (nth 0 '(a b c))
A
而要找到第 n 個 cdr ,我們呼叫 nthcdr :
> (nthcdr 2 '(a b c))
(C)
nth 與 nthcdr 都是零索引的 (zero-indexed); 即元素從 0 開始編號,而不是從 1 開始。在 Common Lisp 裡,無論何時你使用一個數字來參照一個資料結構中的元素時,都是從 0 開始編號的。
兩個函數幾乎做一樣的事; nth 等同於取 nthcdr 的 car 。沒有檢查錯誤的情況下, nthcdr 可以這麼定義:
(defun our-nthcdr (n lst)
(if (zerop n)
lst
(our-nthcdr (- n 1) (cdr lst))))
函數 zerop 僅在參數爲零時,才返回真。
函數 last 返回列表的最後一個 Cons 物件:
> (last '(a b c))
(C)
這跟取得最後一個元素不一樣。要取得列表的最後一個元素,你要取得 last 的 car 。
Common Lisp 定義了函數 first 直到 tenth 可以取得列表對應的元素。這些函數不是 零索引的 (zero-indexed):
(second x) 等同於 (nth 1 x) 。
此外, Common Lisp 定義了像是 caddr 這樣的函數,它是 cdr 的 cdr 的 car 的縮寫 ( car of cdr of cdr )。所有這樣形式的函數 cxr ,其中 x 是一個字串,最多四個 a 或 d ,在 Common Lisp 裡都被定義好了。使用 cadr 可能會有異常 (exception)產生,在所有人都可能會讀的程式裡,使用這樣的函數,可能不是個好主意。
3.7 映射函數 (Mapping Functions)¶
Common Lisp 提供了數個函數來對一個列表的元素做函數呼叫。最常使用的是 mapcar ,接受一個函數以及一個或多個列表,並返回把函數應用至每個列表的元素的結果,直到有的列表沒有元素爲止:
> (mapcar #'(lambda (x) (+ x 10))
'(1 2 3))
(11 12 13)
> (mapcar #'list
'(a b c)
'(1 2 3 4))
((A 1) (B 2) (C 3))
相關的 maplist 接受同樣的參數,將列表的漸進的下一個 cdr 傳入函數。
> (maplist #'(lambda (x) x)
'(a b c))
((A B C) (B C) (C))
其它的映射函數,包括 mapc 我們在 89 頁討論(譯註:5.4 節最後),以及 mapcan 在 202 頁(譯註:12.4 節最後)討論。
3.8 樹 (Trees)¶
Cons 物件可以想成是二元樹, car 代表左子樹,而 cdr 代表右子樹。舉例來說,列表
(a (b c) d) 也是一棵由圖 3.8 所代表的樹。 (如果你逆時針旋轉 45 度,你會發現跟圖 3.3 一模一樣)
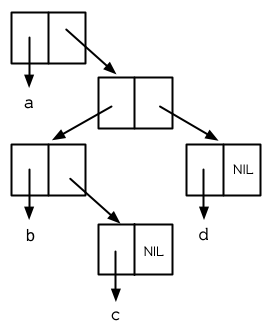
圖 3.8 二元樹 (Binary Tree)
Common Lisp 有幾個內建的操作樹的函數。舉例來說, copy-tree 接受一個樹,並返回一份副本。它可以這麼定義:
(defun our-copy-tree (tr)
(if (atom tr)
tr
(cons (our-copy-tree (car tr))
(our-copy-tree (cdr tr)))))
把這跟 36 頁的 copy-list 比較一下; copy-tree 複製每一個 Cons 物件的 car 與 cdr ,而 copy-list 僅複製 cdr 。
沒有內部節點的二元樹沒有太大的用處。 Common Lisp 包含了操作樹的函數,不只是因爲我們需要樹這個結構,而是因爲我們需要一種方法,來操作列表及所有內部的列表。舉例來說,假設我們有一個這樣的列表:
(and (integerp x) (zerop (mod x 2)))
而我們想要把各處的 x 都換成 y 。呼叫 substitute 是不行的,它只能替換序列 (sequence)中的元素:
> (substitute 'y 'x '(and (integerp x) (zerop (mod x 2))))
(AND (INTEGERP X) (ZEROP (MOD X 2)))
這個呼叫是無效的,因爲列表有三個元素,沒有一個元素是 x 。我們在這所需要的是 subst ,它替換樹之中的元素。
> (subst 'y 'x '(and (integerp x) (zerop (mod x 2))))
(AND (INTEGERP Y) (ZEROP (MOD Y 2)))
如果我們定義一個 subst 的版本,它看起來跟 copy-tree 很相似:
> (defun our-subst (new old tree)
(if (eql tree old)
new
(if (atom tree)
tree
(cons (our-subst new old (car tree))
(our-subst new old (cdr tree))))))
操作樹的函數通常有這種形式, car 與 cdr 同時做遞迴。這種函數被稱之爲是 雙重遞迴 (doubly recursive)。
3.9 理解遞迴 (Understanding Recursion)¶
學生在學習遞迴時,有時候是被鼓勵在紙上追蹤 (trace)遞迴程式呼叫 (invocation)的過程。 (288頁「譯註:附錄 A 追蹤與回溯」可以看到一個遞迴函數的追蹤過程。)但這種練習可能會誤導你:一個程式設計師在定義一個遞迴函數時,通常不會特別地去想函數的呼叫順序所導致的結果。
如果一個人總是需要這樣子思考程式,遞迴會是艱難的、沒有幫助的。遞迴的優點是它精確地讓我們更抽象地來檢視算法。你不需要考慮真正函數時所有的呼叫過程,就可以判斷一個遞迴函數是否是正確的。
要知道一個遞迴函數是否做它該做的事,你只需要問,它包含了所有的情況嗎?舉例來說,下面是一個尋找列表長度的遞迴函數:
> (defun len (lst)
(if (null lst)
0
(+ (len (cdr lst)) 1)))
我們可以藉由檢查兩件事情,來確信這個函數是正確的:
- 對長度爲
0的列表是有效的。 - 給定它對於長度爲
n的列表是有效的,它對長度是n+1的列表也是有效的。
如果這兩點是成立的,我們知道這個函數對於所有可能的列表都是正確的。
我們的定義顯然地滿足第一點:如果列表( lst ) 是空的( nil ),函數直接返回 0 。現在假定我們的函數對長度爲 n 的列表是有效的。我們給它一個 n+1 長度的列表。這個定義說明了,函數會返回列表的 cdr 的長度再加上 1 。 cdr 是一個長度爲 n 的列表。我們經由假定可知它的長度是 n 。所以整個列表的長度是 n+1 。
我們需要知道的就是這些。理解遞迴的祕密就像是處理括號一樣。你怎麼知道哪個括號對上哪個?你不需要這麼做。你怎麼想像那些呼叫過程?你不需要這麼做。
更複雜的遞迴函數,可能會有更多的情況需要討論,但是流程是一樣的。舉例來說, 41 頁的 our-copy-tree ,我們需要討論三個情況: 原子,單一的 Cons 物件, n+1 的 Cons 樹。
第一個情況(長度零的列表)稱之爲基本用例( base case )。當一個遞迴函數不像你想的那樣工作時,通常是因爲基本用例是錯的。下面這個不正確的 member 定義,是一個常見的錯誤,整個忽略了基本用例:
(defun our-member (obj lst)
(if (eql (car lst) obj)
lst
(our-member obj (cdr lst))))
我們需要初始一個 null 測試,確保在到達列表底部時,沒有找到目標時要停止遞迴。如果我們要找的物件沒有在列表裡,這個版本的 member 會陷入無窮迴圈。附錄 A 更詳細地檢視了這種問題。
能夠判斷一個遞迴函數是否正確只不過是理解遞迴的上半場,下半場是能夠寫出一個做你想做的事情的遞迴函數。 6.9 節討論了這個問題。
3.10 集合 (Sets)¶
列表是表示小集合的好方法。列表中的每個元素都代表了一個集合的成員:
> (member 'b '(a b c))
(B C)
當 member 要返回“真”時,與其僅僅返回 t ,它返回由尋找物件所開始的那部分。邏輯上來說,一個 Cons 扮演的角色和 t 一樣,而經由這麼做,函數返回了更多資訊。
一般情況下, member 使用 eql 來比較物件。你可以使用一種叫做關鍵字參數的東西來重寫預設的比較方法。多數的 Common Lisp 函數接受一個或多個關鍵字參數。這些關鍵字參數不同的地方是,他們不是把對應的參數放在特定的位置作匹配,而是在函數呼叫中用特殊標籤,稱爲關鍵字,來作匹配。一個關鍵字是一個前面有冒號的符號。
一個 member 函數所接受的關鍵字參數是 :test 參數。
如果你在呼叫 member 時,傳入某個函數作爲 :test 參數,那麼那個函數就會被用來比較是否相等,而不是用 eql 。所以如果我們想找到一個給定的物件與列表中的成員是否相等( equal ),我們可以:
> (member '(a) '((a) (z)) :test #'equal)
((A) (Z))
關鍵字參數總是選擇性添加的。如果你在一個呼叫中包含了任何的關鍵字參數,他們要擺在最後; 如果使用了超過一個的關鍵字參數,擺放的順序無關緊要。
另一個 member 接受的關鍵字參數是 :key 參數。藉由提供這個參數,你可以在作比較之前,指定一個函數運用在每一個元素:
> (member 'a '((a b) (c d)) :key #'car)
((A B) (C D))
在這個例子裡,我們詢問是否有一個元素的 car 是 a 。
如果我們想要使用兩個關鍵字參數,我們可以使用其中一個順序。下面這兩個呼叫是等價的:
> (member 2 '((1) (2)) :key #'car :test #'equal)
((2))
> (member 2 '((1) (2)) :test #'equal :key #'car)
((2))
兩者都詢問是否有一個元素的 car 等於( equal ) 2。
如果我們想要找到一個元素滿足任意的判斷式像是── oddp ,奇數返回真──我們可以使用相關的 member-if :
> (member-if #'oddp '(2 3 4))
(3 4)
我們可以想像一個限制性的版本 member-if 是這樣寫成的:
(defun our-member-if (fn lst)
(and (consp lst)
(if (funcall fn (car lst))
lst
(our-member-if fn (cdr lst)))))
函數 adjoin 像是條件式的 cons 。它接受一個物件及一個列表,如果物件還不是列表的成員,才構造物件至列表上。
> (adjoin 'b '(a b c))
(A B C)
> (adjoin 'z '(a b c))
(Z A B C)
通常的情況下它接受與 member 函數同樣的關鍵字參數。
集合論中的並集 (union)、交集 (intersection)以及補集 (complement)的實現,是由函數 union 、 intersection 以及 set-difference 。
這些函數期望兩個(正好 2 個)列表(一樣接受與 member 函數同樣的關鍵字參數)。
> (union '(a b c) '(c b s))
(A C B S)
> (intersection '(a b c) '(b b c))
(B C)
> (set-difference '(a b c d e) '(b e))
(A C D)
因爲集閤中沒有順序的概念,這些函數不需要保留原本元素在列表被找到的順序。舉例來說,呼叫 set-difference 也有可能返回 (d c a) 。
3.11 序列 (Sequences)¶
另一種考慮一個列表的方式是想成一系列有特定順序的物件。在 Common Lisp 裡,序列( sequences )包括了列表與向量 (vectors)。本節介紹了一些可以運用在列表上的序列函數。更深入的序列操作在 4.4 節討論。
函數 length 返回序列中元素的數目。
> (length '(a b c))
3
我們在 24 頁 (譯註:2.13節 our-length )寫過這種函數的一個版本(僅可用於列表)。
要複製序列的一部分,我們使用 subseq 。第二個(需要的)參數是第一個開始引用進來的元素位置,第三個(選擇性)參數是第一個不引用進來的元素位置。
> (subseq '(a b c d) 1 2)
(B)
>(subseq '(a b c d) 1)
(B C D)
如果省略了第三個參數,子序列會從第二個參數給定的位置引用到序列尾端。
函數 reverse 返回與其參數相同元素的一個序列,但順序顛倒。
> (reverse '(a b c))
(C B A)
一個迴文 (palindrome) 是一個正讀反讀都一樣的序列 —— 舉例來說, (abba) 。如果一個迴文有偶數個元素,那麼後半段會是前半段的鏡射 (mirror)。使用 length 、 subseq 以及 reverse ,我們可以定義一個函數
(defun mirror? (s)
(let ((len (length s)))
(and (evenp len)
(let ((mid (/ len 2)))
(equal (subseq s 0 mid)
(reverse (subseq s mid)))))))
來檢測是否是迴文:
> (mirror? '(a b b a))
T
Common Lisp 有一個內建的排序函數叫做 sort 。它接受一個序列及一個比較兩個參數的函數,返回一個有同樣元素的序列,根據比較函數來排序:
> (sort '(0 2 1 3 8) #'>)
(8 3 2 1 0)
你要小心使用 sort ,因爲它是破壞性的(destructive)。考慮到效率的因素, sort 被允許修改傳入的序列。所以如果你不想你本來的序列被改動,傳入一個副本。
使用 sort 及 nth ,我們可以寫一個函數,接受一個整數 n ,返回列表中第 n 大的元素:
(defun nthmost (n lst)
(nth (- n 1)
(sort (copy-list lst) #'>)))
我們把整數減一因爲 nth 是零索引的,但如果 nthmost 是這樣的話,會變得很不直觀。
(nthmost 2 '(0 2 1 3 8))
多努力一點,我們可以寫出這個函數的一個更有效率的版本。
函數 every 和 some 接受一個判斷式及一個或多個序列。當我們僅輸入一個序列時,它們測試序列元素是否滿足判斷式:
> (every #'oddp '(1 3 5))
T
> (some #'evenp '(1 2 3))
T
如果它們輸入多於一個序列時,判斷式必須接受與序列一樣多的元素作爲參數,而參數從所有序列中一次提取一個:
> (every #'> '(1 3 5) '(0 2 4))
T
如果序列有不同的長度,最短的那個序列,決定需要測試的次數。
3.12 棧 (Stacks)¶
用 Cons 物件來表示的列表,很自然地我們可以拿來實現下推棧 (pushdown stack)。這太常見了,以致於 Common Lisp 提供了兩個宏給堆疊使用: (push x y) 把 x 放入列表 y 的前端。而 (pop x) 則是將列表 x 的第一個元素移除,並返回這個元素。
兩個函數都是由 setf 定義的。如果參數是常數或變數,很簡單就可以翻譯出對應的函數呼叫。
表達式
(push obj lst)
等同於
(setf lst (cons obj lst))
而表達式
(pop lst)
等同於
(let ((x (car lst)))
(setf lst (cdr lst))
x)
所以,舉例來說:
> (setf x '(b))
(B)
> (push 'a x)
(A B)
> x
(A B)
> (setf y x)
(A B)
> (pop x)
(A)
> x
(B)
> y
(A B)
以上,全都遵循上述由 setf 所給出的相等式。圖 3.9 展示了這些表達式被求值後的結構。
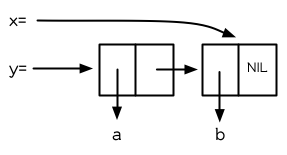
圖 3.9 push 及 pop 的效果
你可以使用 push 來定義一個給列表使用的互動版 reverse 。
(defun our-reverse (lst)
(let ((acc nil))
(dolist (elt lst)
(push elt acc))
acc))
在這個版本,我們從一個空列表開始,然後把 lst 的每一個元素放入空表裡。等我們完成時,lst 最後一個元素會在最前端。
pushnew 宏是 push 的變種,使用了 adjoin 而不是 cons :
> (let ((x '(a b)))
(pushnew 'c x)
(pushnew 'a x)
x)
(C A B)
在這裡, c 被放入列表,但是 a 沒有,因爲它已經是列表的一個成員了。
3.13 點狀列表 (Dotted Lists)¶
呼叫 list 所構造的列表,這種列表精確地說稱之爲正規列表(properlist )。一個正規列表可以是 NIL 或是 cdr 是正規列表的 Cons 物件。也就是說,我們可以定義一個只對正規列表返回真的判斷式: [3]
(defun proper-list? (x)
(or (null x)
(and (consp x)
(proper-list? (cdr x)))))
至目前爲止,我們構造的列表都是正規列表。
然而, cons 不僅是構造列表。無論何時你需要一個具有兩個欄位 (field)的列表,你可以使用一個 Cons 物件。你能夠使用 car 來參照第一個欄位,用 cdr 來參照第二個欄位。
> (setf pair (cons 'a 'b))
(A . B)
因爲這個 Cons 物件不是一個正規列表,它用點狀表示法來顯示。在點狀表示法,每個 Cons 物件的 car 與 cdr 由一個句點隔開來表示。這個 Cons 物件的結構展示在圖 3.10 。
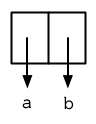
圖3.10 一個成對的 Cons 物件 (A cons used as a pair)
一個非正規列表的 Cons 物件稱之爲點狀列表 (dotted list)。這不是個好名字,因爲非正規列表的 Cons 物件通常不是用來表示列表: (a . b) 只是一個有兩部分的資料結構。
你也可以用點狀表示法表示正規列表,但當 Lisp 顯示一個正規列表時,它會使用普通的列表表示法:
> '(a . (b . (c . nil)))
(A B C)
順道一提,注意列表由點狀表示法與圖 3.2 箱子表示法的關聯性。
還有一個過渡形式 (intermediate form)的表示法,介於列表表示法及純點狀表示法之間,對於 cdr 是點狀列表的 Cons 物件:
> (cons 'a (cons 'b (cons 'c 'd)))
(A B C . D)
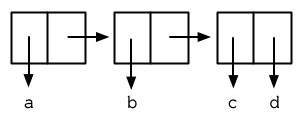
圖 3.11 一個點狀列表 (A dotted list)
這樣的 Cons 物件看起來像正規列表,除了最後一個 cdr 前面有一個句點。這個列表的結構展示在圖 3.11 ; 注意它跟圖3.2 是多麼的相似。
所以實際上你可以這麼表示列表 (a b) ,
(a . (b . nil))
(a . (b))
(a b . nil)
(a b)
雖然 Lisp 總是使用後面的形式,來顯示這個列表。
3.14 關聯列表 (Assoc-lists)¶
用 Cons 物件來表示映射 (mapping)也是很自然的。一個由 Cons 物件組成的列表稱之爲關聯列表(assoc-listor alist)。這樣的列表可以表示一個翻譯的集合,舉例來說:
> (setf trans '((+ . "add") (- . "subtract")))
((+ . "add") (- . "subtract"))
關聯列表很慢,但是在初期的程式中很方便。 Common Lisp 有一個內建的函數 assoc ,用來取出在關聯列表中,與給定的鍵值有關聯的 Cons 對:
> (assoc '+ trans)
(+ . "add")
> (assoc '* trans)
NIL
如果 assoc 沒有找到要找的東西時,返回 nil 。
我們可以定義一個受限版本的 assoc :
(defun our-assoc (key alist)
(and (consp alist)
(let ((pair (car alist)))
(if (eql key (car pair))
pair
(our-assoc key (cdr alist))))))
和 member 一樣,實際上的 assoc 接受關鍵字參數,包括 :test 和 :key 。 Common Lisp 也定義了一個 assoc-if 之於 assoc ,如同 member-if 之於 member 一樣。
3.15 範例:最短路徑 (Example: Shortest Path)¶
圖 3.12 包含一個搜索網路中最短路徑的程式。函數 shortest-path 接受一個起始節點,目的節點以及一個網路,並返回最短路徑,如果有的話。
在這個範例中,節點用符號表示,而網路用含以下元素形式的關聯列表來表示:
(node . neighbors)
所以由圖 3.13 展示的最小網路 (minimal network)可以這樣來表示:
(setf min '((a b c) (b c) (c d)))
(defun shortest-path (start end net)
(bfs end (list (list start)) net))
(defun bfs (end queue net)
(if (null queue)
nil
(let ((path (car queue)))
(let ((node (car path)))
(if (eql node end)
(reverse path)
(bfs end
(append (cdr queue)
(new-paths path node net))
net))))))
(defun new-paths (path node net)
(mapcar #'(lambda (n)
(cons n path))
(cdr (assoc node net))))
圖 3.12 廣度優先搜索(breadth-first search)
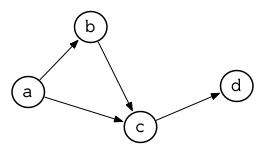
圖 3.13 最小網路
要找到從節點 a 可以到達的節點,我們可以:
> (cdr (assoc 'a min))
(B C)
圖 3.12 程式使用廣度優先的方式搜索網路。要使用廣度優先搜索,你需要維護一個含有未探索節點的佇列。每一次你到達一個節點,檢查這個節點是否是你要的。如果不是,你把這個節點的子節點加入佇列的尾端,並從佇列起始選一個節點,從這繼續搜索。藉由總是把較深的節點放在佇列尾端,我們確保網路一次被搜索一層。
圖 3.12 中的程式較不複雜地表示這個概念。我們不僅想要找到節點,還想保有我們怎麼到那的紀錄。所以與其維護一個具有節點的佇列 (queue),我們維護一個已知路徑的佇列,每個已知路徑都是一列節點。當我們從佇列取出一個元素繼續搜索時,它是一個含有佇列前端節點的列表,而不只是一個節點而已。
函數 bfs 負責搜索。起初佇列只有一個元素,一個表示從起點開始的路徑。所以 shortest-path 呼叫 bfs ,並傳入 (list (list start)) 作爲初始佇列。
bfs 函數第一件要考慮的事是,是否還有節點需要探索。如果佇列爲空, bfs 返回 nil 指出沒有找到路徑。如果還有節點需要搜索, bfs 檢視佇列前端的節點。如果節點的 car 部分是我們要找的節點,我們返回這個找到的路徑,並且爲了可讀性的原因我們反轉它。如果我們沒有找到我們要找的節點,它有可能在現在節點之後,所以我們把它的子節點(或是每一個子路徑)加入佇列尾端。然後我們遞迴地呼叫 bfs 來繼續搜尋剩下的佇列。
因爲 bfs 廣度優先地搜索,第一個找到的路徑會是最短的,或是最短之一:
> (shortest-path 'a 'd min)
(A C D)
這是佇列在我們連續呼叫 bfs 看起來的樣子:
((A))
((B A) (C A))
((C A) (C B A))
((C B A) (D C A))
((D C A) (D C B A))
在佇列中的第二個元素變成下一個佇列的第一個元素。佇列的第一個元素變成下一個佇列尾端元素的 cdr 部分。
圖 3.12 的程式,不是搜索一個網路最快的方法,但它給出了列表具有多功能的概念。在這個簡單的程式中,我們用三種不同的方式使用了列表:我們使用一個符號的列表來表示路徑,一個路徑的列表來表示在廣度優先搜索中的佇列 [4] ,以及一個關聯列表來表示網路本身。
3.16 垃圾 (Garbages)¶
有很多原因可以使列表變慢。列表提供了循序存取而不是隨機存取,所以列表取出一個指定的元素比陣列慢,同樣的原因,錄音帶取出某些東西比在光盤上慢。電腦內部裡, Cons 物件傾向於用指標表示,所以走訪一個列表意味著走訪一系列的指標,而不是簡單地像陣列一樣增加索引值。但這兩個所花的代價與配置及回收 Cons 核 (cons cells)比起來小多了。
自動記憶體管理(Automatic memory management)是 Lisp 最有價值的特色之一。 Lisp 系統維護著一段記憶體稱之爲堆疊(Heap)。系統持續追蹤堆疊當中沒有使用的記憶體,把這些記憶體發放給新產生的物件。舉例來說,函數 cons ,返回一個新配置的 Cons 物件。從堆疊中配置記憶體有時候通稱爲 consing 。
如果記憶體永遠沒有釋放, Lisp 會因爲創建新物件把記憶體用完,而必須要關閉。所以系統必須週期性地通過搜索堆疊 (heap),尋找不需要再使用的記憶體。不需要再使用的記憶體稱之爲垃圾 (garbage),而清除垃圾的動作稱爲垃圾回收 (garbage collection或 GC)。
垃圾是從哪來的?讓我們來創造一些垃圾:
> (setf lst (list 'a 'b 'c))
(A B C)
> (setf lst nil)
NIL
一開始我們呼叫 list , list 呼叫 cons ,在堆疊上配置了一個新的 Cons 物件。在這個情況我們創出三個 Cons 物件。之後當我們把 lst 設爲 nil ,我們沒有任何方法可以再存取 lst ,列表 (a b c) 。 [5]
因爲我們沒有任何方法再存取列表,它也有可能是不存在的。我們不再有任何方式可以存取的物件叫做垃圾。系統可以安全地重新使用這三個 Cons 核。
這種管理記憶體的方法,給程式設計師帶來極大的便利性。你不用顯式地配置 (allocate)或釋放 (dellocate)記憶體。這也表示了你不需要處理因爲這麼做而可能產生的臭蟲。記憶體泄漏 (Memory leaks)以及迷途指標 (dangling pointer)在 Lisp 中根本不可能發生。
但是像任何的科技進步,如果你不小心的話,自動記憶體管理也有可能對你不利。使用及回收堆疊所帶來的代價有時可以看做 cons 的代價。這是有理的,除非一個程式從來不丟棄任何東西,不然所有的 Cons 物件終究要變成垃圾。 Consing 的問題是,配置空間與清除記憶體,與程式的常規運作比起來花費昂貴。近期的研究提出了大幅改善記憶體回收的演算法,但是 consing 總是需要代價的,在某些現有的 Lisp 系統中,代價是昂貴的。
除非你很小心,不然很容易寫出過度顯式創建 cons 物件的程式。舉例來說, remove 需要複製所有的 cons 核,直到最後一個元素從列表中移除。你可以藉由使用破壞性的函數避免某些 consing,它試著去重用列表的結構作爲參數傳給它們。破壞性函數會在 12.4 節討論。
當寫出 cons 很多的程式是如此簡單時,我們還是可以寫出不使用 cons 的程式。典型的方法是寫出一個純函數風格,使用很多列表的第一版程式。當程式進化時,你可以在程式的關鍵部分使用破壞性函數以及/或別種資料結構。但這很難給出通用的建議,因爲有些 Lisp 實現,記憶體管理處理得相當好,以致於使用 cons 有時比不使用 cons 還快。這整個議題在 13.4 做更進一步的細部討論。
無論如何 consing 在原型跟實驗時是好的。而且如果你利用了列表給你帶來的靈活性,你有較高的可能寫出後期可存活下來的程式。
Chapter 3 總結 (Summary)¶
- 一個 Cons 是一個含兩部分的資料結構。列表用鏈結在一起的 Cons 組成。
- 判斷式
equal比eql來得不嚴謹。基本上,如果傳入參數印出來的值一樣時,返回真。 - 所有 Lisp 物件表現得像指標。你永遠不需要顯式操作指標。
- 你可以使用
copy-list複製列表,並使用append來連接它們的元素。 - 遊程編碼是一個餐廳中使用的簡單壓縮演算法。
- Common Lisp 有由
car與cdr定義的多種存取函數。 - 映射函數將函數應用至逐項的元素,或逐項的列表尾端。
- 巢狀列表的操作有時被考慮爲樹的操作。
- 要判斷一個遞迴函數是否正確,你只需要考慮是否包含了所有情況。
- 列表可以用來表示集合。數個內建函數把列表當作集合。
- 關鍵字參數是選擇性的,並不是由位置所識別,是用符號前面的特殊標籤來識別。
- 列表是序列的子型別。 Common Lisp 有大量的序列函數。
- 一個不是正規列表的 Cons 稱之爲點狀列表。
- 用 cons 物件作爲元素的列表,可以拿來表示對應關係。這樣的列表稱爲關聯列表(assoc-lists)。
- 自動記憶體管理拯救你處理記憶體配置的煩惱,但製造過多的垃圾會使程式變慢。
Chapter 3 習題 (Exercises)¶
- 用箱子表示法表示以下列表:
(a) (a b (c d))
(b) (a (b (c (d))))
(c) (((a b) c) d)
(d) (a (b . c) d)
- 寫一個保留原本列表中元素順序的
union版本:
> (new-union '(a b c) '(b a d))
(A B C D)
- 定義一個函數,接受一個列表並返回一個列表,指出相等元素出現的次數,並由最常見至最少見的排序:
> (occurrences '(a b a d a c d c a))
((A . 4) (C . 2) (D . 2) (B . 1))
- 爲什麼
(member '(a) '((a) (b)))返回 nil? - 假設函數
pos+接受一個列表並返回把每個元素加上自己的位置的列表:
> (pos+ '(7 5 1 4))
(7 6 3 7)
使用 (a) 遞迴 (b) 迭代 (c) mapcar 來定義這個函數。
- 經過好幾年的審議,政府委員會決定列表應該由
cdr指向第一個元素,而car指向剩下的列表。定義符合政府版本的以下函數:
(a) cons
(b) list
(c) length (for lists)
(d) member (for lists; no keywords)
勘誤: 要解決 3.6 (b),你需要使用到 6.3 節的參數 &rest 。
- 修改圖 3.6 的程式,使它使用更少 cons 核。 (提示:使用點狀列表)
- 定義一個函數,接受一個列表並用點狀表示法印出:
> (showdots '(a b c))
(A . (B . (C . NIL)))
NIL
- 寫一個程式來找到 3.15 節裡表示的網路中,最長有限的路徑 (不重複)。網路可能包含迴圈。
腳註
| [3] | 這個敘述有點誤導,因爲只要是對任何東西都不返回 nil 的函數,都不是正規列表。如果給定一個環狀 cdr 列表(cdr-circular list),它會無法終止。環狀列表在 12.7 節 討論。 |
| [4] | 12.3 小節會展示更有效率的佇列實現方式。 |
| [5] | 事實上,我們有一種方式來存取列表。全局變數 * , ** , 以及 *** 總是設定爲最後三個頂層所返回的值。這些變數在除錯的時候很有用。 |